今回は、算数・数学の中で、学年をまたがってつまずいてしまうポイントの一つ、
・分数の通分(小学校の算数で初登場)
・分数のある方程式(中学数学)
という、分数が絡む問題を解く際のコツを説明していきます。
分数の通分
まずは、分数の通分から。
例えば、次のような問題。
$$\frac{1}{30}+\frac{1}{45}$$
通分をして解いていきます。
今回の場合は、分母を「90」にそろえます。
$$\frac{1\times3}{30\times3}+\frac{1\times2}{45\times2}=\frac{3}{90}+\frac{2}{90}=\frac{5}{90}$$
約分できるので、
$$\frac{5}{90}=\frac{5\div5}{90\div5}=\frac{1}{18}$$
となります。
最小公倍数
さて、「今、30と45を通分して分母を90に」
と何気なく書きましたが、この90はどのように出せばよいのでしょうか?
慣れればなんとなく、という部分もありますが、
30と45の最小公倍数を探します。
最小公倍数とは、つぎのようなものです。
まず、倍数というのは、
ある整数を1倍・2倍・3倍・・・してできる数のことです。
例えば、
30の倍数・・・30, 60, 90, 120, 150, 180, ……
45の倍数・・・45, 90, 135, 180, ……
となります。
公倍数というのは、共通する倍数のことで、
30と45の公倍数は、太字の数字、つまり、
30と45の公倍数・・・90, 180, 270, ….
となります。
その公倍数のなかで最小のものを、最小公倍数といいます。
30と45の最小公倍数は、「90」となります。
ということで、最小公倍数をみつけるには、頭の中に数字を並べるか書き出すかするればいいのですが、それだと、少し面倒な場合があります。
すだれ算
そこで、すだれ算(連除法/逆割り算/はしご算)を使います。
すだれ算/連除法/逆割り算/はしご算・・・、呼び方はいろいろありますが、全部同じもので、こんなやつです。
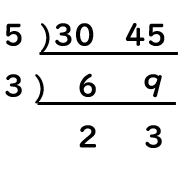
30と45で共通して割れる数で、割っていきます。
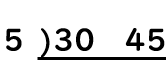
30と45を5で割って、答えをそれぞれ下に書きます。
さらに出た数字を割っていくと、こうなります。
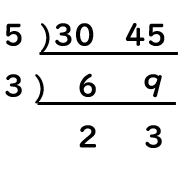
そして、以下の数字に注目します。
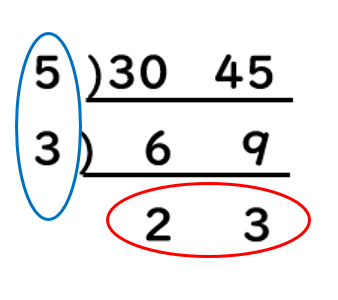
上記の、青と赤で〇をつけた数字を全て掛け算します。
5×3×2×3=5×2×3×3=10×9=90
というように、90と出て、最小公倍数が出てきます。
ちなみに、青丸の部分(5と3)のみを掛け算すると、15となり、最大公約数が出てきます。
方程式で使う
上記の最小公倍数は、分数を含む方程式を解く場合にも使えます。
例えば、次のような問題です。
$$\frac{x}{30}+\frac{x}{45}=5$$
整数にする
分数を含む方程式では、両辺に同じ数をかけて、整数にして、計算しやすくしていきます。
では、何をかければいいのか?
分母の、30と45の最小公倍数90をかければよいのです。
最小公倍数
出し方をおさらいします。
とにかく書き出すか、
30の倍数・・・30, 60, 90, 120, 150, 180, ……
45の倍数・・・45, 90, 135, 180, ……
下記のようにすだれ算を使います。
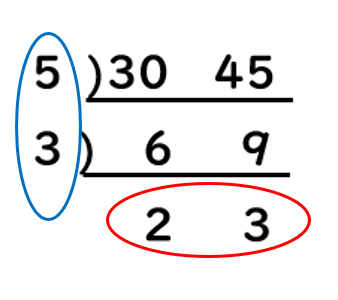
上記の、青と赤で〇をつけた数字を全て掛け算します。
5×3×2×3=5×2×3×3=10×9=90
30と45の最小公倍数は90でした。
では、計算していきます。
$$\frac{x}{30}+\frac{x}{45}=5$$
両辺に90を掛けます。
$$\frac{x}{30}\times90+\frac{x}{45}\times90=5\times90$$
整理して解きます。
$$3x+2x=450$$
$$5x=450$$
$$x=90$$
まとめ
以上のように、ちょっとした工夫で、計算がしやすくなる場面は、かなり多くあります。中学レベルだけではなく、高校内容以上の、高度な内容でも、最難関の入試でも、威力を発揮するものも多くあります。しかもそれが、小学校の内容にさりげなく出ているものだったりします。
ちょっとしたコツが身についていると、できることが広がっていきます。
それにしても、すだれ算/連除法/逆割り算/はしご算・・同じものに、いろいろ名前がありますね。回転焼き/大判焼き/今川焼/おやき/御座候・・・みたいな感じ(?)ですね・・。
いちえいじゅく
一英塾
小学生はガウディア勝田台駅前教室を、中学生・高校生は個別指導教室を開講しています。





TEL:043-463-3003
一英塾(いちえいじゅく)勝田台校
勝田台駅から徒歩2分
千葉県佐倉市井野1544-31
なごみビル202